I came across these websites and was drawn in. They use mathematics to solve seemingly insoluble problems. The first is a medical one - deciding whether (or not) to go ahead with an ablation for paroxysmal atrial fibrillation. The analysis is performed by Tim Gowers, a Fields medal winning Cambridge mathematician, and can be found here.
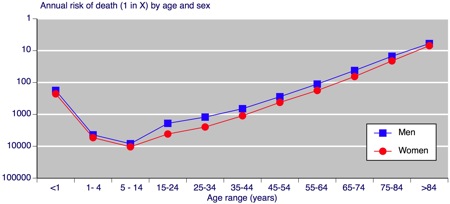
The risk of death is put at one in a thousand, and this is where things get interesting. How worried should I be about a 0.1% risk? How do I even think about that question? Perhaps if my life expectancy from now on is around 30 years, I should think of this as an expected loss of 30/1000 years, or about 10 days. That doesn’t sound too bad — about as bad as having a particularly nasty attack of flu. But is it right to think about it in terms of expectations? I feel that the distribution is important: I would rather have a guaranteed loss of ten days than a 1/1000 chance of losing 30 years.
The data used to estimate the chance of dying within the next 12 months is on the Bandolier site, here.
The second scenario is an intriguing analysis to estimate the possibility of missing a connecting flight against the time it'd take to eat at a favoured airport restaurant - Poisson Eats Cheeseburgers.
It seems a long time since Maths A level, but these sort of posts are rekindling my interest. Check them out for yourself, and also take a look at Numberphile on Youtube.